C Numerical techniques

Recursion (including iteration) combines well with Scheme’s mathematical primitive procedures to implement various numerical techniques. As an example, let’s implement Simpson’s rule, a procedure for finding an approximation for a definite integral.

C.1 Simpson’s rule

The definite integral of a function f(x) within an interval of integration [a,b] can be viewed as the area under the curve representing f(x) from the lower limit x = a to the upper limit x = b. In other words, we consider the graph of the curve for f(x) on the x,y-plane, and find the area enclosed between that curve, the x-axis, and the ordinates of f(x) at x = a and x = b.

According to Simpson’s rule, we divide the interval of integration [a,b] into n evenly spaced intervals, where n is even. (The larger n is, the better the approximation.) The interval boundaries constitute n + 1 points on the x-axis, viz., x₀, x₁, …, x_i, x_i+1, …, x_n, where x₀ = a and x_n = b. The length of each interval is h = (b − a)/n, so each x_i = a + ih. We then calculate the ordinates of f(x) at the interval boundaries. There are n + 1 such ordinates, viz., y₀, …, y_i, …, y_n, where y_i = f(x_i) = f(a + ih). Simpson’s rule approximates the definite integral of f(x) between a and b with the value¹:

${h\over 3} \left[ (y_0 + y_n) + 4(y_1 + y_3 + \cdots + y_{n-1}) + 2(y_2 + y_4 + \cdots + y_{n-2}) \right]$

We define the procedure integrate‑simpson to take four arguments: the integrand f; the x-values at the limits a and b; and the number of intervals n.

(define integrate-simpson
  (lambda (f a b n)
    ;...

The first thing we do in integrate‑simpson’s body is ensure that n is even — if it isn’t, we simply bump its value by 1.

    ;...
    (unless (even? n) (set! n (+ n 1)))
    ;...

Next, we put in the local variable h the length of the interval. We introduce two more local variables h*2 and n/2 to store the values of twice h and half n respectively, as we expect to use these values often in the ensuing calculations.

    ;...
    (let* ((h (/ (- b a) n))
           (h*2 (* h 2))
           (n/2 (/ n 2))
           ;...

We note that the sums y₁ + y₃ + ⋯ + y_n−1 and y₂ + y₄ + ⋯ + y_n−2 both involve adding every other ordinate. So let’s define a local procedure sum‑every‑other‑ordinate‑starting‑from that captures this common iteration. By abstracting this iteration into a procedure, we avoid having to repeat the iteration textually. This not only reduces clutter, but reduces the chance of error, since we have only one textual occurrence of the iteration to debug.

sum‑every‑other‑ordinate‑starting‑from takes two arguments: the starting ordinate and the number of ordinates to be summed.

           ;...
           (sum-every-other-ordinate-starting-from
             (lambda (x0 num-ordinates)
               (let loop ((x x0) (i 0) (r 0))
                 (if (>= i num-ordinates) r
                     (loop (+ x h*2)
                           (+ i 1)
                           (+ r (f x)))))))
           ;...

We can now calculate the three ordinate sums, and combine them to produce the final answer. Note that there are n/2 terms in y₁ + y₃ + ⋯ + y_n−1, and (n/2) − 1 terms in y₂ + y₄ + ⋯ + y_n−2.

           ;...
           (y0+yn (+ (f a) (f b)))
           (y1+y3+...+y.n-1
             (sum-every-other-ordinate-starting-from
               (+ a h) n/2))
           (y2+y4+...+y.n-2
             (sum-every-other-ordinate-starting-from
               (+ a h*2) (- n/2 1))))
      (* 1/3 h
         (+ y0+yn
            (* 4.0 y1+y3+...+y.n-1)
            (* 2.0 y2+y4+...+y.n-2))))))

Let’s use integrate‑simpson to find the definite integral of the function

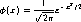
$\phi(x) = {1\over \sqrt{2\pi}} e^{-x^2/2}$

We first define [index-Z-G-D-1.png] in Scheme’s prefix notation.²

(define *pi* (* 4 (atan 1)))

(define phi
  (lambda (x)
    (* (/ 1 (sqrt (* 2 *pi*)))
       (exp (- (* 1/2 (* x x)))))))

Note that we exploit the fact that tan ⁻¹ 1 = [index-Z-G-D-3.png] /4 in order to define *pi*.³

The following calls calculate the definite integrals of phi from 0 to 1, 2, and 3 respectively. They all use 10 intervals.

(integrate-simpson phi 0 1 10)
(integrate-simpson phi 0 2 10)
(integrate-simpson phi 0 3 10)

To four decimal places, these values should be 0.3413, 0.4772, and 0.4987 respectively [2, Table 26.1]. Check to see that our implementation of Simpson’s rule does indeed produce comparable values!⁴

C.2 Adaptive interval sizes

It is not always convenient to specify the number n of intervals. A number that is good enough for one integrand may be woefully inadequate for another. In such cases, it is better to specify the amount of tolerance e we are willing to grant the final answer, and let the program figure out how many intervals are needed. A typical way to accomplish this is to have the program try increasingly better answers by steadily increasing n, and stop when two successive sums differ within e. Thus:

(define integrate-adaptive-simpson-first-try
  (lambda (f a b e)
    (let loop ((n 4)
               (iprev (integrate-simpson f a b 2)))
      (let ((icurr (integrate-simpson f a b n)))
        (if (<= (abs (- icurr iprev)) e)
            icurr
            (loop (+ n 2)))))))

Here we calculate successive Simpson integrals (using our original procedure integrate‑simpson) for n = 2, 4, …. (Remember that n must be even.) When the integral icurr for the current n differs within e from the integral iprev for the immediately preceding n, we return icurr.

One problem with this approach is that we don’t take into account that only some segments of the function benefit from the addition of intervals. For the other segments, the addition of intervals merely increases the computation without contributing to a better overall answer. For an improved adaptation, we could split the integral into adjacent segments, and improve each segment separately.

(define integrate-adaptive-simpson-second-try
  (lambda (f a b e)
    (let integrate-segment ((a a) (b b) (e e))
      (let ((i2 (integrate-simpson f a b 2))
            (i4 (integrate-simpson f a b 4)))
        (if (<= (abs (- i2 i4)) e)
            i4
            (let ((c (/ (+ a b) 2))
                  (e (/ e 2)))
              (+ (integrate-segment a c e)
                 (integrate-segment c b e))))))))

The initial segment is from a to b. To find the integral for a segment, we calculate the Simpson integrals i2 and i4 with the two smallest interval numbers 2 and 4. If these are within e of each other, we return i4. If not we split the segment in half, recursively calculate the integral separately for each segment, and add. In general, different segments at the same level converge at their own pace. Note that when we integrate a half of a segment, we take care to also halve the tolerance, so that the precision of the eventual sum does not decay.

There are still some inefficiencies in this procedure: The integral i4 recalculates three ordinates already determined by i2, and the integral of each half-segment recalculates three ordinates already determined by i2 and i4. We avoid these inefficiencies by making explicit the sums used for i2 and i4, and by transmitting more parameters in the named-let integrate‑segment. This makes for more sharing, both within the body of integrate‑segment and across successive calls to integrate‑segment:

(define integrate-adaptive-simpson
  (lambda (f a b e)
    (let* ((h (/ (- b a) 4))
           (mid.a.b (+ a (* 2 h))))
      (let integrate-segment ((x0 a)
                              (x2 mid.a.b)
                              (x4 b)
                              (y0 (f a))
                              (y2 (f mid.a.b))
                              (y4 (f b))
                              (h h)
                              (e e))
        (let* ((x1 (+ x0 h))
               (x3 (+ x2 h))
               (y1 (f x1))
               (y3 (f x3))
               (i2 (* 2/3 h (+ y0 y4 (* 4.0 y2))))
               (i4 (* 1/3 h (+ y0 y4 (* 4.0 (+ y1 y3))
                               (* 2.0 y2)))))
          (if (<= (abs (- i2 i4)) e)
              i4
              (let ((h (/ h 2)) (e (/ e 2)))
                (+ (integrate-segment
                     x0 x1 x2 y0 y1 y2 h e)
                   (integrate-segment
                     x2 x3 x4 y2 y3 y4 h e)))))))))

integrate‑segment now explicitly sets four intervals of size h, giving five ordinates y0, y1, y2, y3, and y4. The integral i4 uses all of these ordinates, while the integral i2 uses just y0, y2, and y4, with an interval size of twice h. It is easy to verify that the explicit sums used for i2 and i4 do correspond to Simpson sums.

Compare the following approximations of [index-Z-G-D-2.png] ₀²⁰ e^x dx:

(integrate-simpson          exp 0 20 10)
(integrate-simpson          exp 0 20 20)
(integrate-simpson          exp 0 20 40)
(integrate-adaptive-simpson exp 0 20 .001)
(- (exp 20) 1)

The last one is the analytically correct answer. See if you can figure out the smallest n (overshooting is expensive!) such that (integrate‑simpson exp 0 20 n) yields a result comparable to that returned by the integrate‑adaptive‑simpson call.

C.3 Improper integrals

Simpson’s rule cannot be directly applied to improper integrals (integrals such that either the value of the integrand is unbounded somewhere within the interval of integration, or the interval of integration is itself unbounded). However, the rule can still be applied for a part of the integral, with the remaining being approximated by other means. For example, consider the [index-Z-G-D-4.png] function. For n > 0, (n) is defined as the following integral with unbounded upper limit:

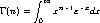
$\Gamma(n) = \int_0^{\infty} x^{n-1}e^{-x} dx$

From this, it follows that (a) [index-Z-G-D-4.png] (1) = 1, and (b) for n > 0, (n + 1) = n(n). This implies that if we know the value of in the interval (1, 2), we can find (n) for any real n > 0. Indeed, if we relax the condition n > 0, we can use result (b) to extend the domain of (n) to include n ≤0, with the understanding that the function will diverge for integer n ≤0.⁵

We first implement a Scheme procedure gamma‑1‑to‑2 that requires its argument n to be within the interval (1, 2). gamma‑1‑to‑2 takes a second argument e for the tolerance.

(define gamma-1-to-2
  (lambda (n e)
    (unless (< 1 n 2)
      (error 'gamma-1-to-2 "argument outside (1, 2)"))
    ;...

We introduce a local variable gamma‑integrand to hold the [index-Z-G-D-4.png] -integrand g(x) = xⁿ⁻¹e^x:

    ;...
    (let ((gamma-integrand
            (let ((n-1 (- n 1)))
              (lambda (x)
                (* (expt x n-1)
                   (exp (- x))))))
          ;...

We now need to integrate g(x) from 0 to [index-Z-G-D-5.png] . Clearly we cannot deal with an infinite number of intervals; we therefore use Simpson’s rule for only a portion of the interval [0, ), say [0, x_c] (c for “cut-off”). For the remaining, “tail”, interval [x_c, ), we use a tail-integrand t(x) that reasonably approximates g(x), but has the advantage of being more tractable to analytic solution. Indeed, it is easy to see that for sufficiently large x_c, we can replace g(x) by an exponential decay function t(x) = y_c e^{−(x − x_c )}, where y_c = g(x_c). Thus:

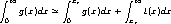
$\int_0^{\infty} g(x) dx \approx \int_0^{x_c} g(x) dx + \int_{x_c}^{\infty} t(x) dx$

The first integral can be solved using Simpson’s rule, and the second integral is just y_c. To find x_c, we start with a low-ball value (say 4), and then refine it by successively doubling it until the ordinate at 2x_c (i.e., g(2x_c)) is within a certain tolerance of the ordinate predicted by the tail-integrand (i.e., t(2x_c)). For both the Simpson integral and the tail-integrand calculation, we will require a tolerance of e/100, an order of 2 less than the given tolerance e, so the overall tolerance is not affected:

          ;...
          (e/100 (/ e 100)))
       (let loop ((xc 4) (yc (gamma-integrand 4)))
         (let* ((tail-integrand
                  (lambda (x)
                    (* yc (exp (- (- x xc))))))
                (x1 (* 2 xc))
                (y1 (gamma-integrand x1))
                (y1-estimated (tail-integrand x1)))
           (if (<= (abs (- y1 y1-estimated)) e/100)
               (+ (integrate-adaptive-simpson 
                    gamma-integrand
                    0 xc e/100)
                  yc)
               (loop x1 y1)))))))

We can now write a more general procedure gamma that returns [index-Z-G-D-4.png] (n) for any real n:

(define gamma
  (lambda (n e)
    (cond ((< n 1) (/ (gamma (+ n 1) e) n))
          ((= n 1) 1)
          ((< 1 n 2) (gamma-1-to-2 n e))
          (else (let ((n-1 (- n 1)))
                  (* n-1 (gamma n-1 e)))))))

Let us now calculate [index-Z-G-D-4.png] (3/2).

(gamma 3/2 .001)
(* 1/2 (sqrt *pi*))

The second value is the analytically correct answer. (This is because [index-Z-G-D-4.png] (3/2) = (1/2)(1/2), and (1/2) is known to be [index-Z-G-D-3.png] ^1/2.) You can modify gamma’s second argument (the tolerance) to get as close an approximation as you desire.

¹ Consult any elementary text on the calculus for an explanation of why this approximation is reasonable.

² [index-Z-G-D-1.png] is the probability density of a random variable with a normal or Gaussian distribution, with mean = 0 and standard deviation = 1. The definite integral [index-Z-G-D-2.png] ₀^z (x) dx is the probability that the random variable assumes a value between 0 and z. However, you don’t need to know all this in order to understand the example!

³ If Scheme didn’t have the atan procedure, we could use our numerical-integration procedure to get an approximation for [index-Z-G-D-2.png] ₀¹ (1 + x²)⁻¹ dx, which is [index-Z-G-D-3.png] /4.

⁴ By pulling constant factors — such as (/ 1 (sqrt (* 2 *pi*))) in phi — out of the integrand, we could speed up the ordinate calculations within integrate‑simpson.

⁵ [index-Z-G-D-4.png] (n) for real n > 0 is itself an extension of the “decrement-then-factorial” function that maps integer n > 0 to (n−1)!.